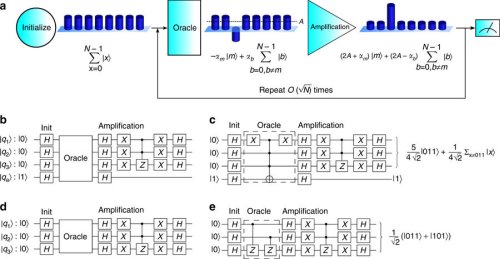
Осуществление поиска по большим базам неупорядоченных данных является очень затратной операцией с точки зрения времени и ресурсов для классических компьютеров, но квантовые компьютеры, как ожидается, будут справляться с таким поиском намного быстрей за счет особенностей их функционирования и использования специальных алгоритмов. Из этих квантовых алгоритмов самым быстрым считается алгоритм поиска Гровера, предложенный еще в 1996 году. Это означает, что никакой другой квантовый алгоритм не сможет выполнить процедуру поиска быстрей, чем алгоритм Гровера. Однако, практическая реализация алгоритма Гровера на реальной квантовой вычислительной системе сама по себе является достаточно сложной задачей.
Не так давно группа исследователей из университета Мэриленда, при поддержке американского Национального научного фонда, успешно реализовала алгоритм поиска Гровера на системе, использующей в качестве кубитов пойманные в ловушку ионы. Эта система состояла из трех кубитов, что позволяло ей производить поиск по базе, состоящей из 8 (2^3) элементов. При этом, алгоритм Гровера обеспечил поиск элемента за один, максимум за две итерации (прохода), показав результат, намного превосходящий даже теоретический показатель успешности для традиционных компьютеров.
Классическим подходом к поиску в неструктурированной базе является прямой перебор. В большинстве случаев алгоритм выбирает любой из элементов базы случайным образом. Если выбранный элемент не является искомым, то все действия повторяются, а вероятность нахождения искомого элемента из восьми после второго прохода (итерации) равна 25 процентам.
Алгоритм Гровера, с другой стороны, переводит квантовую систему в такое положение суперпозиции, когда в ней находятся сразу все 8 значений данных, среди которых находится и искомое значение. Затем алгоритм задействует особую функцию, называемую оракулом, которая по ряду критериев отмечает искомое значение. В результате такого "квантового" подхода теоретический показатель вероятности нахождения искомого значения сразу на первом проходе составляет 78 процентов, а на втором проходе эта вероятность составляет уже все 100 процентов. Это, в свою очередь, определяет малое время, требующееся для нахождения искомого значения.
При практическом выполнении алгоритм поиска Гровера показал на первом проходе более низкое значение показателя успешности, которое оказалось гораздо ниже теоретического значения и составило 39 и 44 процента в зависимости от вида используемой функции-оракула. Тем не менее, такой показатель значительно превышает аналогичный показатель успешности обычных компьютеров.
Исследователи так же проверили работу алгоритма поиска Гровера на наборах данных, содержащих по два правильных решения. В таком случае теоретические показатели успешности на первом проходе для классических и квантовых компьютеров составляют 47 и 100 процентов соответственно. И снова практический показатель успешности оказался ниже теоретического и составил 68 и 75 процентов для двух типов функций-оракулов.
"В будущем мы собираемся реализовать алгоритм Гровера на большее количество кубитов, что позволит осуществлять поиск по базам данных больших объемов" - пишут исследователи, - "Помимо этого мы работаем над созданием новой квантовой системы, в которой будет реализован лучший уровень управления кубитами, которые, к тому же, будут качественней ограждены от нежелательных воздействий из окружающей среды. Это, в свою очередь, позволит такой квантовой системе продемонстрировать показатели успешности поиска решения, равные или близкие к теоретическим значениям".
